GANs #003 Autoencoder implemented with TensorFlow 2.0
Highlights: In this post we will talk about autoencoders. In particular, you will gain a deeper insight into the working mechanisms of autoencoders. They are important machine learning models for data compression, analysis and data modeling.
Moreover, we will present several autoencoder architectures and show how they can be implemented in TensorFlow 2.0. So, let’s get started.
Tutorial Overview:
1. Methodology
Our goal in generative modeling is to find ways to learn the hidden variables when we are only given the observed data.
An autoencoder is a very simple generative model which tries to learn the underlying latent variables in the data by coding its input.
If they are so simple, how do they work?
The simplest version of an autoencoder can be just a neural network with a single hidden layer. This hidden layer connects the input and the output. An output is not known (unsupervised learning), but should be such that it reconstructs the input vector. The following image explains this concept nicely.

We first begin by feeding raw input data into the model which is passed through one (or more) neural network layers. The output of the hidden layer is what we call an encoder, or a low dimensional latent space. It is a feature vector representation that we are trying to reveal.

Specifically, this network is an encoder because it maps the input data \(x \) into a vector of latent variables \(z \).
Why do we care about this low dimensional latent space?
Well, it can be very useful for the compression of our data. Furthermore, this step can also be useful for data visualization (e.g. similar as with PCA). Moreover, the holy grail that we are searching for are compact and distinctive features. And last but not least, autoencoders are used for image denoising and reconstruction (image inpainting). Hence, those are the main applications of autoencoders.
To illustrate this topic further, when we work with images, a pixel-based space is very highly dimensional. So, our goal is to take that high dimensional information and encode it into a compressed latent vector representation.
Our next question is: How do we train the weights of a neural network to get this latent variable vector \(z \)? Well, the problem is that we never actually have access to this data (hence the name hidden 🙂 ), since we cannot directly observe it. Recall the cocktail party problem and the sound of a piano that we cannot measure directly. Even if we put hundreds of microphones, a piano tune is still going to be mixed with other sound sources in the room.
Hence, we do not have labeled data and we cannot cast this encoding process as a supervised learning problem. However, we can find a solution for this by adding a decoder structure. In more simple words, a decoder will now be the fully connected neural network or a convolutional neural network. The goal of the decoder would be to reconstruct a replica of the original image from this learned latent space.
In other words, with an image example we can simply take the mean squared error from the input to the reconstructed image at the output. Here, the really important thing is that the loss function doesn’t have any labels. So, this is an unsupervised learning problem. The only components of the loss are the input \(x \) and the reconstructions \(\hat{x}\).
\(mse = (\frac{1}{n})\sum_{i=1}^{n}( x _{i} – \hat{x} _{i})^{2} \)

The output of the decoder network we will call the reconstructed output \(\hat{x}\)
Remind you of anything?
So, this is going to be a lossy reconstruction of the original input \(x \). You have maybe noticed the similarity to the concept of PCA. We can reduce the number of dimensions, and as a result the reconstructed data cannot be perfectly reconstructed (lossy compression).
Hence, this network will be trained using the reconstruction error as our objective function. That is, we want the input \(x \) and our reconstructed output \(\hat{x}\) to be as similar as possible. In addition, pay special attention to this part: the key concept here is that from a reduced set of variables, vector \(z\), we need to reconstruct the output \(\hat{x}\) which will be of a much higher dimension. This is not an easy task!

Well, we know this was indeed a lot of theory.
Finally, it’s time for some coding.
2. Implementation in TensorFlow 2.0
# General libraries
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# Libraries for autoencoding
from tensorflow.keras import datasets
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Reshape
# Libraries for PCA
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# Importing the image data and normalizing
(X_train, y_train), (X_test, y_test) = datasets.mnist.load_data()
X_train, X_test = X_train / 255.0, X_test / 255.0
# Try different sizes!
size_hidden_layer = 20
# Encoder with just one hidden layer
class Encoder(Sequential):
def __init__(self):
super().__init__()
self.add(Flatten(input_shape=(28, 28)))
self.add(Dense(size_hidden_layer, activation='relu'))
# Decoder with a dense layer with 28x28 units.
class Decoder(Sequential):
def __init__(self):
super().__init__()
self.add(Dense(784, activation='sigmoid',
input_shape=[size_hidden_layer]))
self.add(Reshape([28, 28]))
encoder = Encoder()
decoder = Decoder()
# Autoencoder can be created as a sequential model with
# encoder and decoder.
autoencoder = Sequential([encoder, decoder])
autoencoder.compile(loss= 'mean_squared_error',
optimizer= SGD(1.5),
metrics=['accuracy'])
# Note that here X_test is not obligatory.
autoencoder_hidden_layer_results = autoencoder.fit(X_train, X_train,
epochs= 5)
# Prediction for the first 10 images
X_rec_autoencoder = autoencoder.predict(X_test[:10])
# Now let's do the same for PCA
X_train = X_train.reshape([X_train.shape[0], X_train.shape[1] * X_train.shape[2]])
X_test = X_test.reshape([X_test.shape[0], X_test.shape[1] * X_test.shape[2]])
n_components = 20
pca = PCA(n_components=n_components)
pca.fit(X_train)
num_elements = X_test.shape[0]
X_test_PCA = pca.fit_transform(X_test)
X_rec_pca = pca.inverse_transform(X_test_PCA)
X_rec_pca = np.reshape(X_rec_pca[:10], (10,28,28))
X_test = np.reshape(X_test[:10], (10,28,28))
# Function for plotting the data and results
def plotter(data, title):
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(10):
ax = fig.add_subplot(1, 10, i + 1, xticks=[], yticks=[])
ax.imshow(data[i],
cmap=plt.cm.binary, interpolation='nearest')
ax.yaxis.set_label_position("right")
ax.set_ylabel(title, fontsize='medium')
# Now let's see how the predictions look
# Along with the difference from the original
plotter(X_test,'X_test')
plotter(X_rec_autoencoder,'Autoencoder')
plotter(X_rec_pca,'PCA')Output:
Epoch 1/5
1875/1875 [==============================] – 3s 2ms/step – loss: 0.0643 – accuracy: 0.1061
Epoch 2/5
1875/1875 [==============================] – 3s 2ms/step – loss: 0.0405 – accuracy: 0.1734
Epoch 3/5
1875/1875 [==============================] – 3s 2ms/step – loss: 0.0342 – accuracy: 0.1973
Epoch 4/5
1875/1875 [==============================] – 3s 2ms/step – loss: 0.0304 – accuracy: 0.2092
Epoch 5/5
1875/1875 [==============================] – 3s 2ms/step – loss: 0.0278 – accuracy: 0.2171
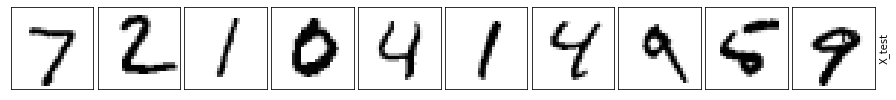


This example shows that even the simplest autoencoder, that has only a single hidden layer unit, outperforms the standard PCA algorithm. This should not come as a surprise, as we actually have nonlinear data modeling compared to linear PCA.
>>here an image from edureka and linear/vs/nonlinear PCA problem <<
| Type | Bottleneck layers size | Error |
|---|---|---|
| Simple autoencoder | 400-200-100-50-30-50-100-200-400 | 0.0295 |
| Simple autoencoder | 400-200-100-50-25-50-100-200-400 | 0.0295 |
| Simple autoencoder | 400-200-100-50-20-50-100-200-400 | 0.0307 |
| Simple autoencoder | 400-200-100-50-10-50-100-200-400 | 0.0302 |
The autoencoders cannot just be taken “off-the shelf”. There is some work that we need to engineer. The most important detail is how we select the dimensionality of our latent space. This is the, so called, hidden bottleneck layer and its size represents a trade-off between the feature compactness, compression and accuracy of the reconstruction. The lower the size, the higher the reconstruction error will be, and vice versa. One approach for this would be to use a well known Akaike Information Criterion (AIC) and plot this value versus the number of features. For more information see Data Science Handbook, GMM example.
Code
Let’s see how this model will perform on the FashionMNIST dataset.
# General libraries
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# Libraries for autoencoding
from tensorflow.keras import datasets
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Reshape
# Importing the image data and normalizing
(X_train, y_train), (X_test, y_test) = datasets.fashion_mnist.load_data()
X_train, X_test = X_train / 255.0, X_test / 255.0
class Encoder(Sequential):
def __init__(self):
super().__init__()
self.add(Flatten(input_shape=(28, 28)))
self.add(Dense(400, activation='relu'))
self.add(Dense(200, activation='relu'))
self.add(Dense(100, activation='relu'))
self.add(Dense(50, activation='relu'))
self.add(Dense(25, activation='relu'))
class Decoder(Sequential):
def __init__(self):
super().__init__()
self.add(Dense(50, activation='relu', input_shape=[25]))
self.add(Dense(100, activation='relu'))
self.add(Dense(200, activation='relu'))
self.add(Dense(400, activation='relu'))
self.add(Dense(784, activation='sigmoid'))
self.add(Reshape([28, 28]))
encoder = Encoder()
decoder = Decoder()
autoencoder = Sequential([encoder, decoder])
autoencoder.compile(loss= 'mean_squared_error',
optimizer= SGD(1.5))
autoencoder_result = autoencoder.fit(X_train, X_train,
epochs= 5)
X_rec_autoencoder = autoencoder.predict(X_test[:10])
# This will show the difference
# between the test and prediction
diff_autoencoder = X_rec_autoencoder - X_test[:10]
# Function for plotting the data and results
def plotter(data, title):
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(10):
ax = fig.add_subplot(1, 10, i + 1, xticks=[], yticks=[])
ax.imshow(data[i],
cmap=plt.cm.binary, interpolation='nearest')
ax.yaxis.set_label_position("right")
ax.set_ylabel(title, fontsize='medium')
# Now let's see how the prediction looks with this dataset
# Along with the difference from the original
plotter(X_test,'X_test')
plotter(X_rec_autoencoder,'Autoencoder')
plotter(diff_autoencoder, 'Difference Autoencoder')Output:
Epoch 1/5
1875/1875 [==============================] – 14s 7ms/step – loss: 0.0569
Epoch 2/5
1875/1875 [==============================] – 14s 7ms/step – loss: 0.0330
Epoch 3/5
1875/1875 [==============================] – 14s 7ms/step – loss: 0.0266
Epoch 4/5
1875/1875 [==============================] – 14s 7ms/step – loss: 0.0246
Epoch 5/5
1875/1875 [==============================] – 14s 7ms/step – loss: 0.0231



As you can see, important details are lost using a simple autoencoder. Let’s continue with building more complex models.
Convolutional layer autoencoder
In addition, the autoencoder can be constructed from fully connected (dense) Neural Networks layers, but we can also use convolutional layers as well as many deep learning architectures.
The encoder network, in this case, will resemble the classical model \(conv net\) from a Deep Neural Network. However, the novelty can be seen in the part of the decoder network. Let us recall that in the \(conv nets\) we are decreasing the image-pixel size using convolution (‘same’ convolutions decreases the number of features ) and max pooling. On the other hand, the decoder network will start from our latent vector \(z \) (e.g. a vector of size 10), and from this vector, we need to reconstruct the original image (e.g. 28×28 image pixels).
In order to achieve this, it is necessary to create an upsampling layer. Here, we present the code snippet and display how easily it can be applied and what the expected output is:
Code
tf.keras.layers.UpSampling2D(
size=(2, 2), data_format=None, interpolation='nearest', **kwargs
)Expected Output
In this MNIST example, we can see the original digits from this dataset. We show an example of how reconstructed images will look like in a 2D latent space. We can see a great improvement if we increase the latent vector size and go to a 5D latent space. The quality of this reconstruction is indeed much better.
Code
# General libraries
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# Libraries for Conv
from tensorflow.keras import datasets
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Reshape
from tensorflow.keras.layers import Conv2D, MaxPooling2D, UpSampling2D
# Libraries for PCA
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# Importing the data and normalizing it
(X_train, y_train), (X_test, y_test) = datasets.mnist.load_data()
X_train, X_test = X_train / 255.0, X_test / 255.0
# Preparing the data
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1], X_train.shape[2], 1)
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1], X_test.shape[2], 1)
print(X_train.shape)
print(X_test.shape)
class Encoder(Sequential):
def __init__(self):
super().__init__()
# Notice the Conv2D layers
self.add(Conv2D(16, (3, 3), activation='relu', padding='same'))
self.add(MaxPooling2D((2, 2), padding='same'))
self.add(Conv2D(8, (3, 3), activation='relu', padding='same'))
self.add(MaxPooling2D((2, 2), padding='same'))
self.add(Conv2D(8, (3, 3), activation='relu', padding='same'))
self.add(MaxPooling2D((2, 2), padding='same'))
class Decoder(Sequential):
def __init__(self):
super().__init__()
# Adding the Conv2D layers to the decoder as well
self.add(Conv2D(8, (3, 3), activation='relu', padding='same'))
self.add(UpSampling2D((2, 2)))
self.add(Conv2D(8, (3, 3), activation='relu', padding='same'))
self.add(UpSampling2D((2, 2)))
self.add(Conv2D(16, (3, 3), activation='relu'))
self.add(UpSampling2D((2, 2)))
self.add(Conv2D(1, (3,3), activation='sigmoid', padding='same'))
encoder = Encoder()
decoder = Decoder()
autoencoder = Sequential([encoder, decoder])
autoencoder.compile(loss= 'mean_squared_error',
optimizer= SGD(1.5),
metrics=['accuracy'])
autoencoder_conv_results = autoencoder.fit(X_train, X_train,
epochs= 5)
image_batch = autoencoder.predict(X_test[:10])
#Let's see how PCA compares now:
X_train = X_train.reshape([X_train.shape[0], X_train.shape[1] * X_train.shape[2]])
X_test = X_test.reshape([X_test.shape[0], X_test.shape[1] * X_test.shape[2]])
n_components = 20
pca = PCA(n_components=n_components)
pca.fit(X_train)
num_elements = X_test.shape[0]
X_test_PCA = pca.fit_transform(X_test)
X_rec_pca = pca.inverse_transform(X_test_PCA)
X_rec_pca = np.reshape(X_rec_pca[:10], (10,28,28))
X_test = np.reshape(X_test[:10], (10,28,28))
# The function is a little different here than in the previous examples
def plotter(data, title):
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(10):
ax = fig.add_subplot(1, 10, i + 1, xticks=[], yticks=[])
ax.imshow(data[i].reshape(28,28),
cmap=plt.cm.binary, interpolation='nearest')
ax.yaxis.set_label_position("right")
ax.set_ylabel(title, fontsize='medium')
plotter(X_test, 'X_test')
plotter(image_batch, 'Autoencoder conv')
plotter(X_rec_pca, 'PCA')Output:
(60000, 28, 28, 1)
(10000, 28, 28, 1)
Epoch 1/5
1875/1875 [==============================] – 87s 46ms/step – loss: 0.0357 – accuracy: 0.7998
Epoch 2/5
1875/1875 [==============================] – 87s 46ms/step – loss: 0.0231 – accuracy: 0.8069
Epoch 3/5
1875/1875 [==============================] – 87s 47ms/step – loss: 0.0201 – accuracy: 0.8086
Epoch 4/5
1875/1875 [==============================] – 87s 46ms/step – loss: 0.0184 – accuracy: 0.8096
Epoch 5/5
1875/1875 [==============================] – 87s 46ms/step – loss: 0.0172 – accuracy: 0.8103
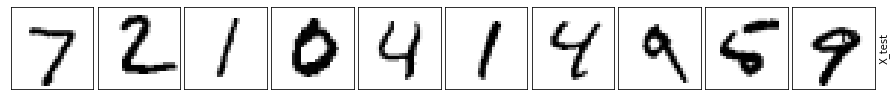
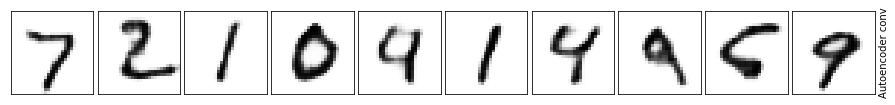

What a difference! The background is much cleaner when we use the convolution layers and the numbers are much more visible. Not to mention it’s closer to the original.
Another popular method for building neural networks is using model subclassing. Let’s see how it can be done in this way.
# So, this is exactly the same as the first way, which is also the easiest one.
# The only difference is we're building the model using model subclassing with Keras.
import matplotlib.pyplot as plt
from tensorflow.keras import Model
from tensorflow.keras import datasets
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.layers import Dense, Flatten, Reshape
# Creating an encoder
class Encoder(Model):
def __init__(self):
super(Encoder, self).__init__()
self.flatten = Flatten(input_shape=(28, 28))
self.dense_1 = Dense(400, activation='relu')
self.dense_2 = Dense(200, activation='relu')
self.dense_3 = Dense(100, activation='relu')
self.dense_4 = Dense(50, activation='relu')
self.dense_5 = Dense(25, activation='relu')
def call(self, x):
x = self.flatten(x)
x = self.dense_1(x)
x = self.dense_2(x)
x = self.dense_3(x)
x = self.dense_4(x)
return self.dense_5(x)
# Creating a decoder
class Decoder(Model):
def __init__(self):
super(Decoder, self).__init__()
self.dense_1 = Dense(50, activation='relu', input_shape=[25])
self.dense_2 = Dense(100, activation='relu')
self.dense_3 = Dense(200, activation='relu')
self.dense_4 = Dense(400, activation='relu')
self.dense_5 = Dense(784, activation='sigmoid')
self.reshape = Reshape([28, 28])
def call(self, x):
x = self.dense_1(x)
x = self.dense_2(x)
x = self.dense_3(x)
x = self.dense_4(x)
x = self.dense_5(x)
return self.reshape(x)
# Creating the model
class Autoencoder(Model):
def __init__(self):
super(Autoencoder, self).__init__()
self.encoder = Encoder()
self.decoder = Decoder()
def call(self, input_features):
code = self.encoder(input_features)
reconstructed = self.decoder(code)
return reconstructed
# Create an instance of the model
autoencoder = Autoencoder()
autoencoder.compile(loss= 'mean_squared_error',
optimizer= SGD(1.5),
metrics=['accuracy'])
# Importing the image data and normalizing
(X_train, y_train), (X_test, y_test) = datasets.mnist.load_data()
X_train, X_test = X_train / 255.0, X_test / 255.0
autoencoder.fit(X_train, X_train,
epochs= 5)
# Prediction for the first 10 images
X_keras_autoencoder = autoencoder.predict(X_test[:10])
# Function for plotting the data and results
def plotter(data, title):
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(10):
ax = fig.add_subplot(1, 10, i + 1, xticks=[], yticks=[])
ax.imshow(data[i],
cmap=plt.cm.binary, interpolation='nearest')
ax.yaxis.set_label_position("right")
ax.set_ylabel(title, fontsize='medium')
# Now let's see how the prediction looks
plotter(X_test,'X_test')
plotter(X_keras_autoencoder,'Autoencoder keras')Output:
Epoch 1/5
1875/1875 [==============================] – 14s 7ms/step – loss: 0.0691 – accuracy: 0.0744
Epoch 2/5
1875/1875 [==============================] – 13s 7ms/step – loss: 0.0527 – accuracy: 0.1192
Epoch 3/5
1875/1875 [==============================] – 14s 7ms/step – loss: 0.0423 – accuracy: 0.1612
Epoch 4/5
1875/1875 [==============================] – 13s 7ms/step – loss: 0.0346 – accuracy: 0.1896
Epoch 5/5
1875/1875 [==============================] – 14s 7ms/step – loss: 0.0308 – accuracy: 0.2014
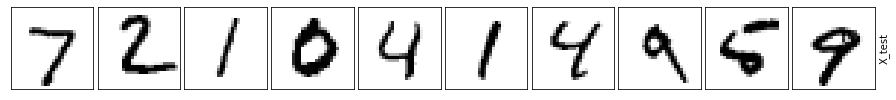

So how do all these autoencoders compare?
| Autoencoder | Loss | Learning time (seconds) |
| One hidden layer (size 20) | 0.0278 | 15 |
| Multilayer | 0.0280 | 72 |
| Conv2D | 0.0172 | 435 |
| Keras | 0.0308 | 68 |
Visually, the autoencoder with convolution layers certainly gives a better result. When it comes to loss, it also beats all the others by having the smallest error. However, it takes a bit more time to learn.
Summary
To sum things up, autoencoders are using the bottleneck hidden layer that forces the network to learn a compressed latent representation of the data. By using this reconstruction loss, we can train the network in a completely unsupervised manner, which is where the name auto encoder comes from: the fact that we’re automatically encoding information within the data into this smaller latent space.
