#003 Linearna diskriminaciona analiza
Klasifikacija
Zamislimo da imamo dve klase, čiji su elementi prikazani kao zvezdice i trouglovi. Cilj mašinskog učenja je da se za ove 2 klase odredi funkcija (crna linija na slici) koja će na optimalan način razdvojiti ove klase. Kada se pojavi novi element, algoritam treba da prepozna sa koje strane ove funkcije će se on nalaziti. Na taj način, novi, do sada nepoznat element (podatak) biće klasifikovan. Najjednostavniji oblik funkcije je linearna funkcija (npr. jednačina prave).
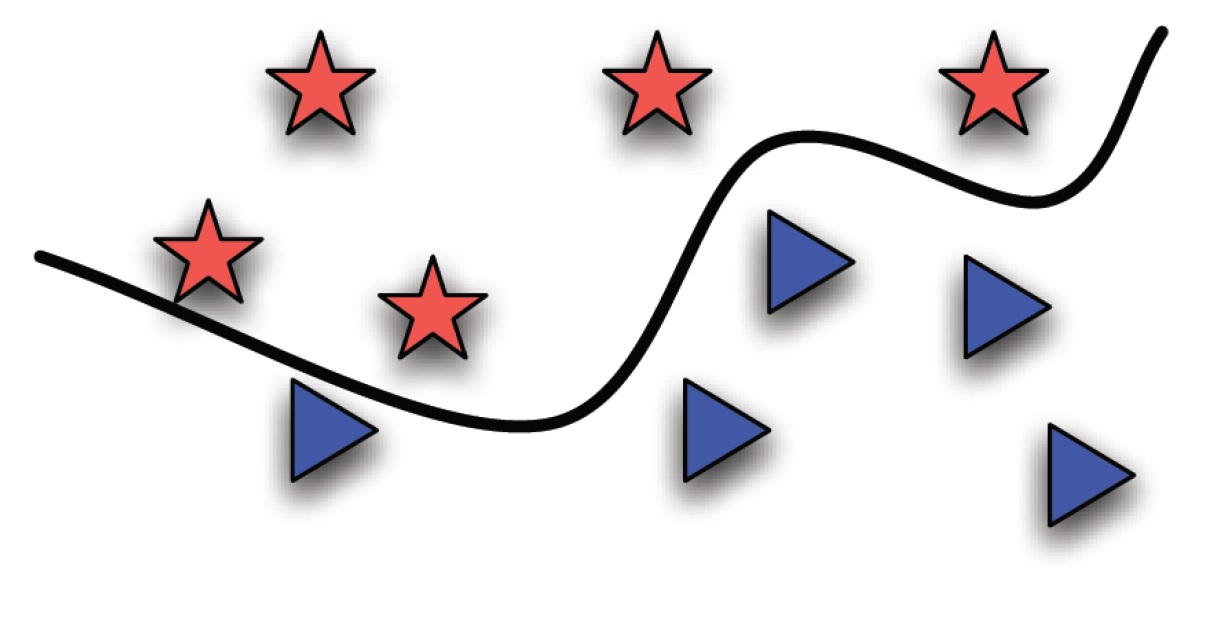
Linearno neseparabilni skupovi
Možemo primetiti da je u našem primeru predložena funkcija “kriva linija” i da prava ne može idealno razdvojiti zvezdice od trouglića. Za ovakva dva skupa elemenata kažemo da su linearno neseparabilni.
Posmatrajmo sada dva skupa tačaka koji jesu linearno separabilni. Ovo je najlakše ilustrovati u samom Python-u:
Dakle, napravili smo matricu X sa 6 redova (horizontalno) i 2 kolone (vertikalno). Sada je bitno pogledati kako se pristupa elementima matrice. U ovom slučaju potrebno je da definišemo dve koordinate da bismo pristupili elementima. Horizontalna koordinata je axis-0, dok je vertikalna axis-1 u Python-u. Indeksiranje počinje nulom, a na sledećoj slici vidimo kako možemo pristupiti pojedinačnim elementima.
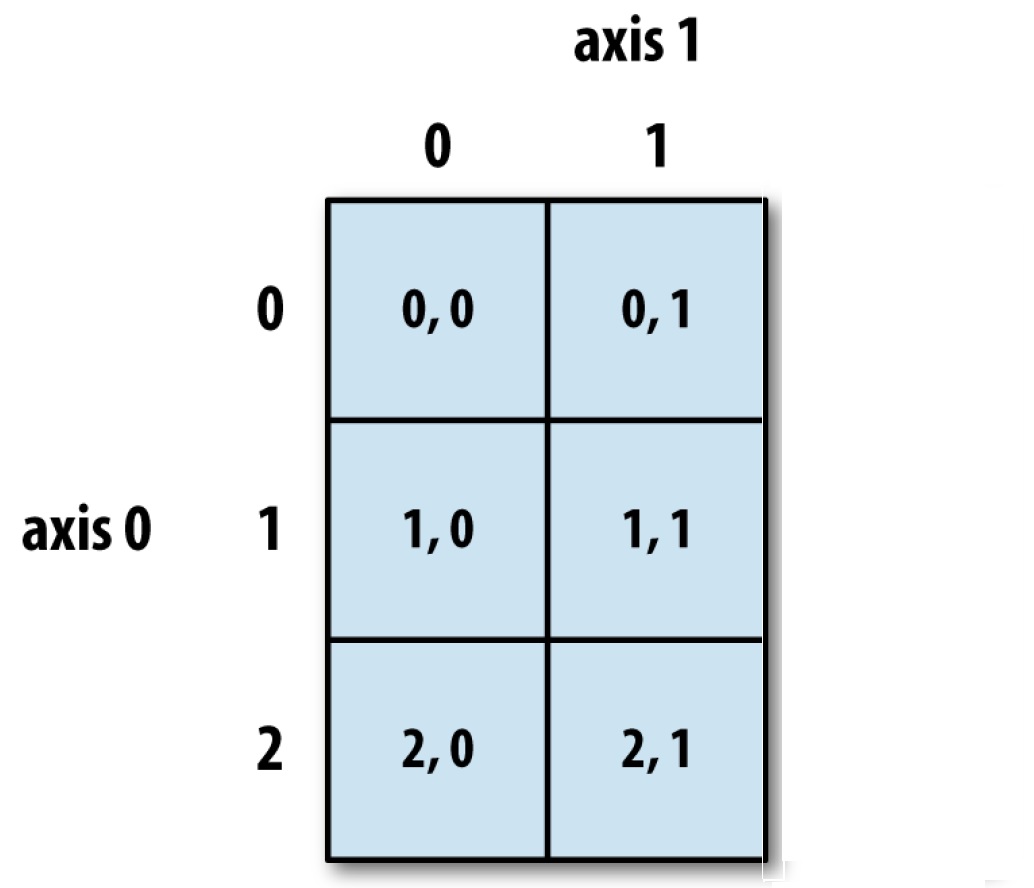
Matrica X
Stoga, X[0, 0] će biti prvi gornji element levo, dok će X[0, 1] prvi gornji desno.
Naredbom X[:,0] selektovaćemo celu prvu kolonu, a naredbom X[:,1] ćemo selektovati celu drugu.
Upravo u ovim nizovima se i nalaze naše koordinate (na grafiku je prva horizontalna, a druga vertikalna). U ovom primeru koristićemo naredbu scatter, koja podatke iscrtava na tačnim koordinatama bez njihovog spajanja.
Ovaj veoma jednostavan skup je linearno separabilan i sastoji se od dve klase, sa po tri elementa. Definišimo sada jednu pravu liniju koja će ova dva skupa tačaka da podeli u dve klase.
Ako se podsetimo linearne algebre, to bi bila prava oblika:
\( x_{2} = kx_{1} + n \)
Ukoliko za vrednost k uzmemo -1, a za n vrednost 1, dobićemo jednačinu: \( x_{2} = -x_{1} +1\)
Jedan od načina da nacrtamo ovu pravu u Python-u je da definišemo neke vrednosti promenljive x1, a da potom izračunamo x2.
Pošto radimo sa nizovima, oba možemo iscrtati jer su istih dužina. To ćemo uraditi sledećim naredbama:
Novodobijena crvena prava deli skup na dva dela, ali je intuitivno jasno da ona nije izabrana kao optimalna.
\(x_{2}= – x_{1} + 1\)
koju sada možemo napisati i u obliku:
\( x_{1} + x_{2} – 1 = 0 \)
odnosno, u formi funkcije: \( f(x_{1},x_{2}) = x_{1}+x_{2} -1 \) definisaće se pripadnost klasi 1 ili klasi 2.
Tako za tačku (1,1) imamo: \( f(1,1) = 1 + 1 – 1 = 1 >0 \) Dakle, ova tačka će biti iznad ravni kao što je ilustrovano na slici i pripadaće klasi 1.
Za tačke ispod ove prave, vrednost ove funkcije će biti manja od nule. Na primer: \( f(-2, -1) = -2 – 1- 1 = -4 \)
Sada dolazimo do osnovne ideje mašinskog učenja. Za novu tačku, na primer sa koordinatama (2, 0) izračunaćemo vrednosti funkcije f(x1, x2). Ova vrednost je: \( f(2, 0) = 2 + 0 – 1 = 1 > 0 \) Ova tačka će pripadati klasi 1.
Ovo je suština mašinskog učenja. Potrebno je izračunati parametre funkcije, u ovom slučaju su to bili parametri (k i n). Nove podatke koristimo za izračunavanje vrednosti ove funkcije i tako dobijamo klasifikaciju posmatrajući da li je ova vrednost manja ili veća od nule.
Naš jednostavan primer upravo je osnova za mnoge druge sofisticirane i složene sisteme za klasifikaciju.
Obratimo pažnju šta je ovde naučeno, tj. zašto se ova oblast zove Machine Learning? Mi smo “naučili” koeficijente k i n i tako dobili našu funkciju f (engl. decision boundary function). Ovde smo ih odredili ručno, a sada ćemo videti kako nam neki algoritmi mogu pomoći da ove parametre određujemo automatski i na optimalan način poštujući neke kriterijumske funkcije.
Linearna diskriminaciona analiza
U prethodnom primeru smo jednostavno odredili koeficijente prave jer je naš problem bio linearno separabilan i imao je samo 6 elemenata. Linearna diskriminaciona analiza (engl. LDA – Linear Discriminant Analysis ) predstavlja alogoritam koji određuje koeficijente prave k i n. Prava će biti postavljena tako da su centri dve klase što je moguće više razmaknuti u odnosu na ovu liniju.
Za definisan skup podataka X, potrebno je odrediti pripadnost klasama. U ovom problemu imamo dve klase koje razmatramo, a možemo ih numerički označiti sa 1 i 2. Kako se skup podataka sastoji od 6 elemenata, potrebno je definisati vektor (NumPy array) tako da prva tri elementa pripadaju klasi 1, a preostala 3 klasi 2.
Vektor y označava pripadnost klasi i kada imamo ovu informaciju možemo vršiti klasifikaciju. Ovo predstavlja nadgledano učenje (engl. supervised learning). Ukoliko nemamo informaciju o pripadnosti klasi koristimo drugu grupu algoritama i vršimo klasterovanje (engl. clustering). Za naše potrebe, koristićemo biblioteku sklearn na kojoj se zasnivaju algoritmi koje ćemo koristiti.
clf je sada naš objekat u kome su smešteni parametri za naš klasifikator. Prva najvažnija metoda je naredba .fit(X, y). Ovom naredbom prosleđuju se objektu clf, ulazni podaci X, kao i vektor klasne pripadnosti y. Ispis out[12] za sada ne moramo analizirati.
Naredbom .fit() podesili smo parametre našeg linearnog klasifikatora. Sada ga možemo testirati za nove elemente koje nismo do sada koristili.
Za podatak (-2, -3) dobili smo da pripada klasi 1. Rezultat je niz sa jednim elementom čija je vrednost 1.
Tražene tačke koje smo testirali možemo prikazati na novom grafiku.