#008 3D Face Modeling – How to Construct a Parametric Face Model?

Highlights: Hello and welcome. In this post, we are going to learn how to construct a parametric face model. We will review famous parametric face model papers that are extremely popular and impactful to this day. The ideas covered in these works encouraged further development of the parametric face models. So, let’s begin with our post.
In this post, we are going to review the YouTube video “3D Scanning & Motion Capture: 8. Parametric Face Models”[1]. So let’s begin!
Blanz and Vetter Morphable Model

First, let’s talk about Blanz and Vetter paper published in 1999. This paper is still extremely popular and this was one of the first ideas that encouraged the development of the parametric face models. The idea here is that we have neutral 3D scans with a very high-quality scanner of human faces. In this case, we take 100 male, and 100 female candidates that we want to scan, and it is assumed that all faces have the same expression.
Note that we’re not yet considering the expressions at this stage. So, this model is only doing neutral faces right now. Also in this paper, authors use two independent PCA models, one for the identity, and one for the albedo.
The idea here is that the sliders that we covered in this post are coefficients that are attached to the eigenvectors from this PCA model. The most important fact is that we can control these sliders. In the following example, we can see that the first slider has the most variation. Therefore it will make the biggest changes. Every other slider will have a smaller and smaller effect on the final output.
Drawbacks
However, we have to be very careful here because we’re talking about human faces, and this work does not represent a distribution of all human faces. So, there’s actually a massive bias in these 200 scans. It consists of mainly Caucasian faces and very few Asian and African faces. So, it’s a problem using the data in the sense that we cannot expect to use all humans.
Furthermore, we also have another drawback. Since this is a PCA basis, one parameter has a global influence. In other words, if we want to just change a wrinkle in the face, it’s not going to be that easy. We will have to change a lot of parameters in this PCA basis to get this desired effect because a single parameter in the PCA basis is always going to affect the whole face.
Blandshapes model
Since this paper is published, there have been many works that have expanded on it. One very popular word that has to be mentioned here is Blandshapes. Blendshapes (known as blend shapes on Maya or morph targets on 3DS Max) are commonly used in 3D animation tools, though their name varies from one 3D software to another. They use the deformations of a 3D shape to show different expressions. Blandshapes are probably still state-of-the-art right now which most people are using for face modeling and face reconstruction.
There is a core difference between this model and Blanz and Vetter, and this is the idea that this is an additive model. So, what does it mean that you have an additive model? Well, it means that instead of modeling a PCA basis of all of these independent faces, we start with a neutral face first. Let’s take a look at the following image.
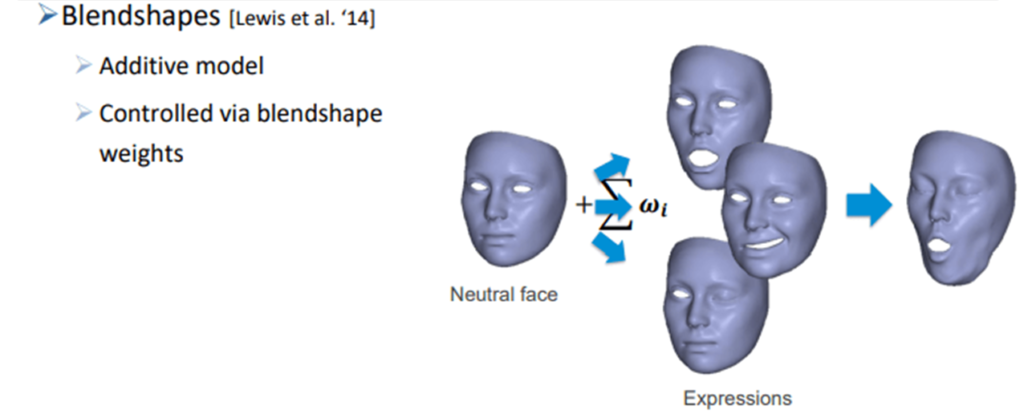
The idea here is that from this neutral face, we’re adding weights respectively, in order to get the expression. So, we have offset vectors, that are controlled via blendshape weights. These blendshape weights represent the sum that can be computed as a linear combination between different scans of one person.
What’s really important for the creation of the parametric face model is that we have two parts:
- We have this morphable model that is defining the shape and the albedo.
- Then, we have the blendshapes that define the expressions.
Overview of the parametric model papers
Now, let’s give a quick overview of the other papers about parametric models.
Human faces are really important for many applications. This is why we want to very briefly give you an overview of the literal landscape that has been done there. Let’s take a look at the following image.
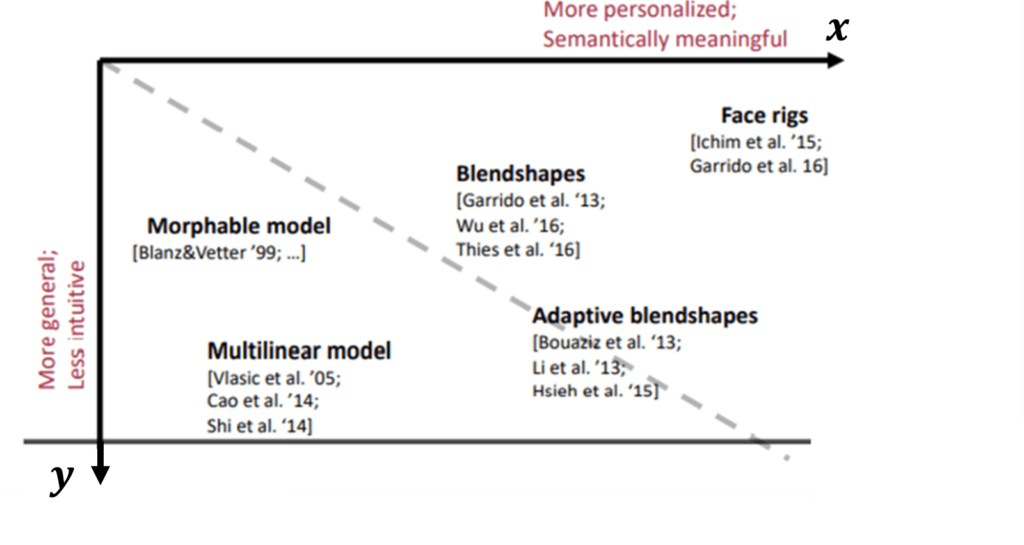
Here, we can see the \(x \) and the \(y \) axis. The \(y \) is the general axis that represents whether the model is more intuitive. On the other hand, the \(x \) is the semantic access that represents whether the model is more or less semantically meaningful. Furthermore, we can see a number of different models. So, if you’re thinking about the Morphable model, we can see that it is not that intuitive and has no semantics. We also have these blendshapes, that are more semantically meaningful.
If we’re looking at these publications, they’re ending around 2017. Since that there’s been a lot of work with deep learning. However, a lot of facial reconstruction is still being done with these classical models.
Parametric Face Model – model construction and fitting
Let’s continue with our post. In the following image, we can see our amazing parametric face model.
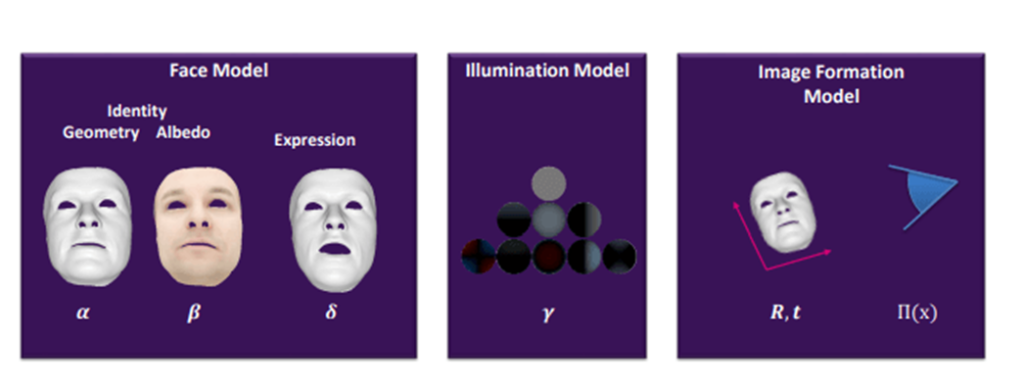
This image represents the summary of our parametric face model with a lot of parameters. Now we’re going to talk about how faces can be reconstructed in practice.
Typically, in this parametric model, we have two parts. Let’s have a look at the following image.
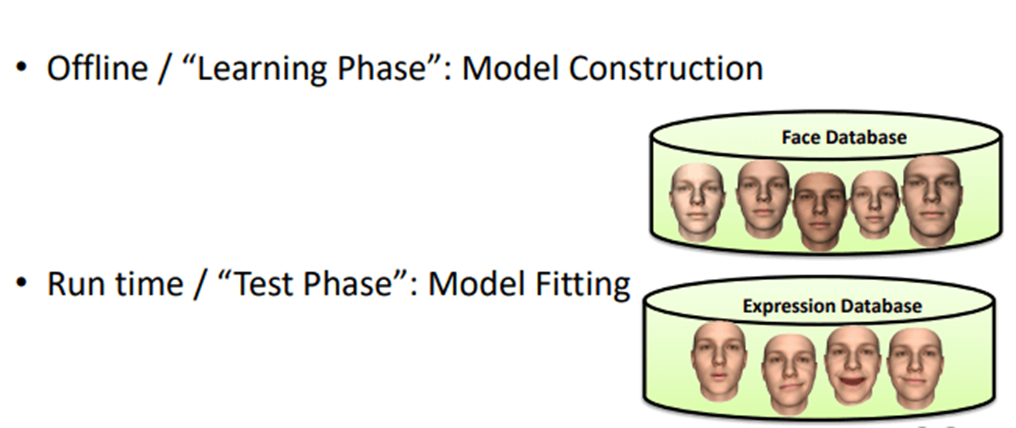
The first part is this offline face that we call a constructor. Once we’ve contracted our face models we can use them at runtime, in order to fit the models to some targets. In a sense, it’s a little bit like machine learning, The first part is a learning phase, and then we have a test phase where we can fit the model to some target image.
Let’s talk about this learning phase and model construction. So, here we want to build a PCA model. In order to do that, let’s just make one assumption. We assume we have a set of meshes of the face with the same topology but different poses. Then, we have 1:1 correspondences between the vertices. Note that basis functions are given through PCA of mesh (linear model).
Now, we can compute the face functions of a PCA-based model. That gives us essentially our face parameters model. So we take these one-to-one correspondences, and we compute the PCA with vertices.
Now, let’s see how we can construct our model.
How to Construct a Parametric Face Model?
Unfortunately, it’s not a straightforward task. The hard part is that we have to find a way for us to get the set of meshes with the same topology, and with one-to-one correspondences in different poses. Then once we have that, we can go ahead and compute the space prior. We can divide this process into the following steps:
Compute face prior:
- Scan a few hundred faces/expressions and fit a topologically-consistent template to each scan using non-rigid registration
- Compute PCA-basis for identity and expressions
At runtime: fit prior to input data
- From a sparse set of keypoints
- From depth data
- From RGB data
So, we want to compute the space prior by scanning a lot of different people. Let’s say we scan 100 people.

Next, we want to hire an artist, which is going to model us a really high-quality face template. Then, we’re not going to non-rigidly register against each of these scans independently. So in practice, that’s what we’re getting here from the scans. Take a look at the following image

These are the scans we typically get. Based on these laser scanners, we’re getting the geometry and we also are getting a rough color approximation. So, we can take two examples as a target to align this artist model template mesh.
Moreover, we don’t actually have to do this with a laser scanner. We can do this with commodity sensors too.


So, we could take a Kinect fusion scan of a static person and just get a static reconstruction of this one person in one pose. Then we can align the template mesh against those examples respectively. This work is called a Face Warehouse. This is particularly interesting because this work actually has a little bit more diversity than the other ones. There are a lot of Asians in this database, and they have more scans.
Let’s have a look at the next image.

Here’s an interesting example that highlights a deformation error. In the first example, we can see a template mesh trying to get aligned and this looks pretty good. However, in the second example, we can see the hair here doesn’t quite fit. We have a high error here.
So, this is our template mesh, being non-rigidly registered successfully by using all the techniques that we already covered. The next step is to take all the vertices of this template mesh and write them as a vector \(V \).

In the image above we can see those vectors. Values of this vector are vertices of the deformed template mash. These template meshes have the same topology, so the dimensionality of these two vectors is going to be the same.
Now, we apply the same process for every frame. Next, we need to compute the PCA. To better understand the process of PCA check out this [link].
In our case, the PCA basis is doing exactly what we’re looking for. We are figuring out which of these axes has the highest variations respectively in the shape or the albedo space.

Note that all the sliders that we showed you in this post are simply the coefficients of the eigenvectors of the spaces. And the PCA is independently computed for the shapes and for the albedo. Once we have it, new faces can be simply computed using a linear combination of these basis vectors.
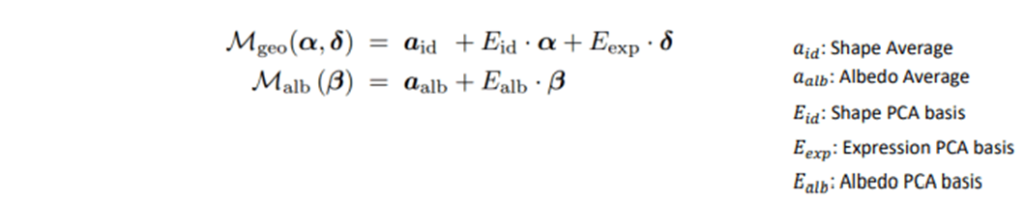
The one thing that is interesting, is the number of principal components here, goes down very quickly.

In the beginning, the first few principal components matter the most, and then they get smaller and smaller. The first principal components represent the most variance, so they make up for the most changes in the face parameters model. This property is kind of interesting because we can basically reduce compute time. And we can use only the first 80 principal components.
Now, let’s move on to the expressions. Here we can apply the same idea. We connect fusion scans for each of the different expressions, Then we can do the very same thing, and that is PCA representation.

Summary
That is it for this post. Here, we talked about several parametric face model papers. In the next lecture, we’re going to talk about how can we reconstruct a given image or a video sequence. In other words, we will explain how we can find the parameters \(P \), that define the face reconstruction for this parametric model.
References:
[1] – 3D Scanning & Motion Capture: 8. Parametric Face Models – Prof. Matthias Nießner