#002 Machine Learning – Linear Regression Models
Highlights: Welcome back to the all-new series on Machine Learning. In the previous post, we gave you a sneak peak into the basics of Machine Learning, the two types of Machine Learning, viz., Supervised & Unsupervised, and implemented some examples using various algorithms in each of the techniques.
In this new tutorial post, we will explore one of the most widely used Supervised Learning algorithms in the world today – Linear Regression. We will start off with some theory and go on to build a simple model in Python, from scratch. So, let’s begin!
Tutorial Overview:
- Linear Regression: Conceptual Basics
- Calculating The Cost Function
- Applying Gradient Descent
- Implementing A Linear Regression Model In Python (From Scratch)
1. Linear Regression: Conceptual Basics
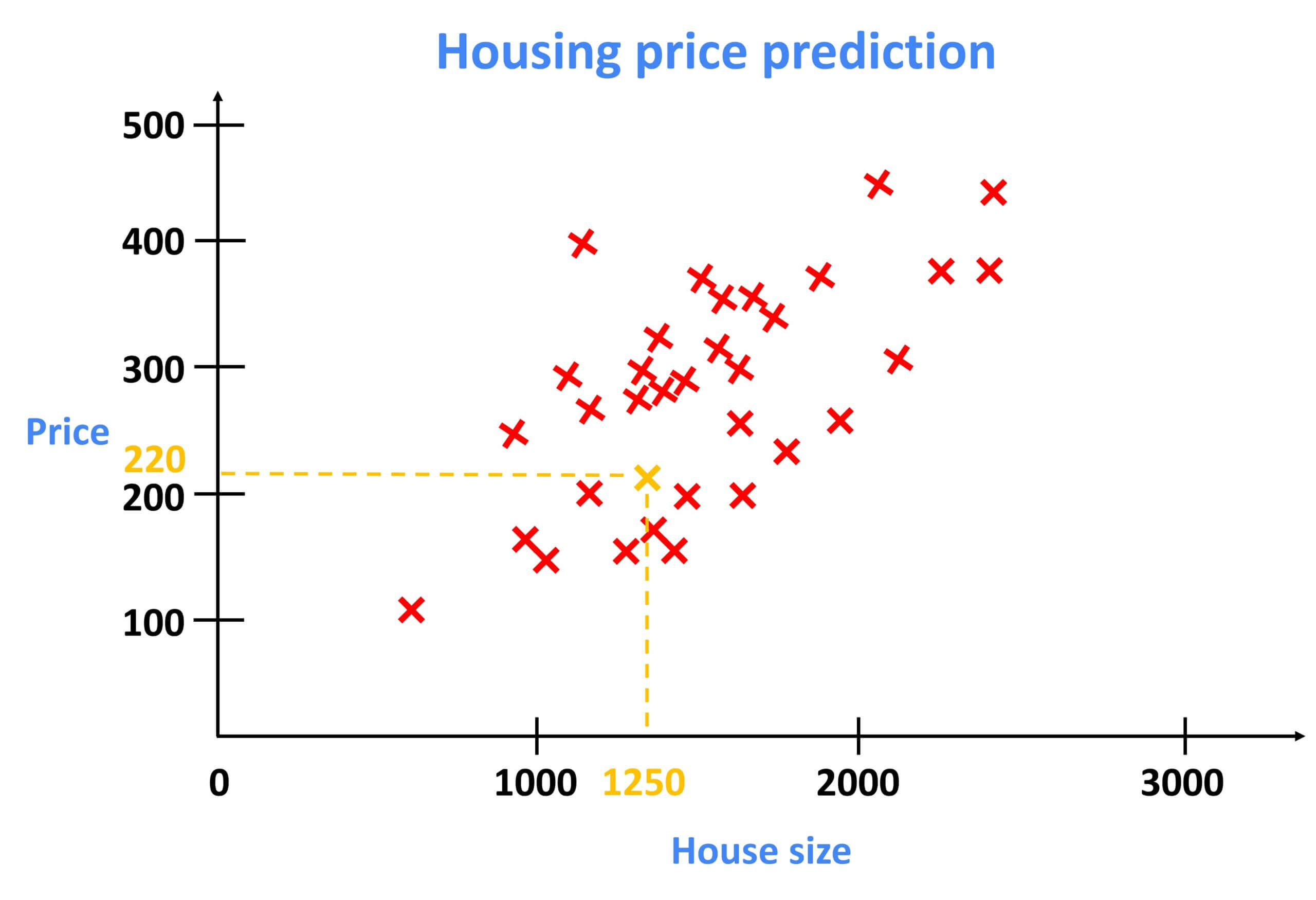
In our previous post (also the first post of this Machine Learning tutorial series), we brushed the fundamentals of Linear Regression using the example of housing price prediction, given the size of the house. If you remember, the prediction was based on the linear relationship that existed between the house price and the size of the house. Have a look at the image below.
In the graph above, the size of the house is shown along the horizontal axis and the price of a house is shown along the vertical axis.
Here, each data point is a house with its respective size and the price that the house was recently sold for.
Now, let’s say you’re a real estate agent and you’re helping a client to sell her house. This dataset might help you estimate the price the client could get for it. You start by measuring the size of the house, and it turns out that the house is 1250 square meters. How much do you think this house could sell for?
One thing you could do is build a Linear Regression model from this dataset. Your model will fit a straight line to the data, which might look something like this.
Based on this straight line fit to the data, you can see that for a house of 1250 square meters size, the price is about $220,000.
In addition to visualizing this data as a plot, there’s another way of looking at the data that would be useful, and that’s a data table.
The data comprises a set of inputs. In the first column, we have the size of the house, and in the second we have the price of the house. Notice that the horizontal and vertical axes on the graph correspond to these two columns, the size, and the price. For example, If you have 30 rows in this data table, then there will be 30 data points on the graph.
The dataset that you just saw and that is used to train the model is called a Training Set. Note that your client’s house is not in this dataset because it’s not yet sold, so no one knows what the price is. To predict the price of your client’s house, you first have to train your model to learn from the training set. In turn, the trained model will, then, be able to predict your client’s house’s price.
Now, let’s look at some notations for describing the data. These notations will be very useful for you throughout your journey in Machine Learning.
- \(x \) – This is the standard notation to denote an input in Machine Learning. We call this the input variable. It is also called an input feature. In this example, \(x \)t is the size of the house.
- \(y \) – This is the standard notation to denote the output variable which you’re trying to predict, which is also sometimes called the target variable. Here, \(y \) is the price of the house.
- \(m \) – The dataset has one row for each house and in this training set, there are 30 rows with each row representing a different training example. We’re going to use lowercase \(m \) to represent the total number of training examples.
- \((x,y) \) – This notation is used to indicate a single training example.
- \((x^{(i)},y^{(i)}) \) – Now, we have 30 different training examples. To refer to a specific training example, we are going to use this notation. The superscript tells us that this is the i-th training example, where \(i \)i refers to a specific row in the table. It is important to note that this superscript in parentheses is not exponentiation. It just refers to the second training example.
Now, let us refresh our memory from our previous post and remember how Supervised Learning works.
A Supervised Learning algorithm will input a training set that includes both the input features, such as the size of the house and also the output targets, such as the price of the house.
The output targets are the right answers to the model we’ll learn from. To train the model, we feed the training set, both the input features and the output targets to your learning algorithm. As a result, the Supervised Learning algorithm will produce some function \(f \).
The job of the function is to take a new input \(x \) and an estimated output \(y \) or a prediction, which we are going to call \(\hat{y} \). It’s written like the variable \(y \) with this little hat symbol on top. In machine learning, the convention is that \(\hat{y} \) is the estimate or the prediction for \(y \). So, the function \(f \) is called the model, \(x\) is called the input or the input feature, and the output of the model is the prediction \(\hat{y} \).
One key question we are trying to answer while designing a learning algorithm is how to represent our function \(f \)? To simply put, what is the math formula we’re going to use to compute the function? In linear regression, we are fitting a straight line into the data. Therefore, the function can be written as:
$$ f_{w,b}(x) = wx+b $$
Here, the variable \(w \) represents the slope of the line, and the variable \(b \) is the point where line intercepts the \(y \) axis.
The values chosen for \(w \) and \(b \) will determine the prediction \(\hat{y} \) based on the input feature \(x \). This term \(f_{w,b}(x) \) means that \(f \) that takes \(x \) as input, and depending on the values of \(w \) and \(b \), it will output some value of a prediction \(\hat{y} \).
Now, our goal here is to apply Linear Regression in order to model the relationship size of the house and the price of the house. To do this, we can draw a line that best fits our dataset. In such a way, we can predict where the future points may be and we can also identify outliers.
However, we have a problem!
We can’t draw the line because the parameters \(w \) and \(b \) are unknown to us. Therefore, the main goal of our analysis is to determine the values for \(w \) and \(b \). In this way, we will be able to find a function of the line which will help us determine the optimal correlation between dependent and independent variables in our model.
Now, let us understand the very first step of designing a Linear Regression model which is essential to improving its efficiency.
2. Calculating The Cost Function
In order to implement Linear Regression, we need to first define a Cost Function. The Cost Function will tell us how well the model is doing so that we can try to get it to do better. Let’s understand using an example.
Understanding The Mathematics
Recall that we have a training set that contains input features \(x \) and output targets \(y \).
The model you’re going to use to fit this training set is this linear function \(f_{w,b}(x) = wx+b \). The variables \(w \) and \(b \) are called the parameters of the model. In machine learning parameters of the model are the variables you can adjust during training in order to improve the model. Sometimes, the parameters \(w \) and \(b \) are also called coefficients or weights. Let’s take a look at what these parameters do.
Depending on the values you’ve chosen for \(w \) and \(b \) we will get a different function \(f(x) \), which generates a different line on the graph. Have a look at the following image.
In the first example, when \(w=0 \), and \(b=1.5 \), the \(f(x) \) comes out to be horizontal because it is always a constant value. It always predicts 1.5 for the \(\hat{y} \).
In the second example, when \(w=0,5 \) and \(b=0 \), then \(f(x)=0 \) for \(x=0 \), \(f(x)=0.5 \) for \(x=1 \), and \(f(x)=1 \) for \(x=2 \). Notice that the slope is equal to 0.5 divided by 1. Here, the value of the slope is equal to 0.5 divided by 1. So, the value of \(w \) gives us the slope of the line, which is 0.5.
Finally, in the third example, when \(w=0.5 \) and \(b=1 \), then, \(f(x)=1 \) for \(x=0 \), \(f(x)=1.5 \) for \(x=1 \), and \(f(x)=2 \) for \(x=2 \). So, the line intersects the vertical axis at \(b \) and the slope is equal to 0.5.
Our training set can be represented as shown in the image below.
With linear regression, what you want to do is to choose values for the parameters \(w \) and \(b \) so that the straight line you get from the function \(f \) somehow fits the data well. The line is passing through or somewhere close to the training examples as compared to other possible lines that are not as close to these points.
Now, the question is how do you find values for \(w \) and \(b \) such that the prediction \(\hat{y}^{(i)} \) is close to the true target \(y^{(i)} \). To answer the question, let’s first take a look at how to measure how well a line fits the training data. To do this, let us construct a Cost Function.
The Cost Function takes the difference between prediction \(\hat{y}^{(i)} \) and the target \(y^{(i)} \). This difference is called the error. We’re measuring how far off to prediction is from the target. Next, we take the square of this error. We’re also going to compute this term for different training examples \(i \) in the training set. Finally, we want to measure the error across the entire training set. Therefore, we will sum up all squared errors.
Notice that if we have more training examples \(m \), the error will be larger and your Cost Function will calculate a bigger number. To build a Cost Function that doesn’t automatically get bigger as the training set size gets larger by convention, we will compute the average squared error instead of the total squared error.
Also by convention, the Cost Function that is used in machine learning is actually divided by \(2m \). In this way, some of our later calculations will look neater, but the Cost Function still works whether you include this division by 2 or not. Let’s write down our equation now.
$$ J(w,b)=\frac{1}{2m}\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)})^{2} $$
This expression is the Cost Function.
This is also called the Squared Error Cost Function because we’re taking the square of these error terms. In Machine Learning, different people will use different cost functions for different applications, but the Squared Error Cost Function is by far the most commonly used for linear regression and in fact, for all regression problems where it seems to give good results for many applications.
Building The Intuition
We saw how a Cost Function can be defined mathematically. But, what really is the Cost Function doing? Let’s try to understand this more intuitively.
Now, Linear Regression would try to find values for\(w \), and \(b \), then make a \(J(w,b) \) as small as possible. In other words, our goal is to minimize \(J(w,b) \). Mathematically, it is written in the following way.
In order for us to better visualize the Cost Function \(J \), we will use a simplified version of the Linear Regression model, as expressed below.
$$ f(x) = wb $$
$$ b=0 $$
You can think of this as taking the original model and setting the parameter \(b =0 \). Now, we have just one parameter \(w \), and our cost function \(J \) looks like this:
$$ J(w)=\frac{1}{2m}\sum_{i=1}^{m}(f_{w}(x^{(i)})-y^{(i)})^{2} $$
With this simplified model, the goal is to find the value of \(w \) that minimizes \(J(w) \). Now, using this simplified model, let’s see how the cost function changes as you choose different values for the parameter \(w \).
In particular, let’s look at graphs of the model \(f(x) \), and the Cost Function \(J \). We are going to plot these side-by-side so that we can closely observe how the two are related.
In the image above, we can see plots these two functions, \(f(x) = wb \), and \(J(w)=\frac{1}{2m}\sum_{i=1}^{m}(f_{w}(x^{(i)})-y^{(i)})^{2} \) side-by-side.
On the left side, we have our model. Here, we can see the plots of three points representing the training set at positions \((1, 1) \), \((2, 2) \), and \((3, 3) \).
Now, let’s pick a random value for \(w \). Let’s say that \(w=1 \). For this choice of \(w \), the function \(f(x) \), is this straight line with a slope of 1.
Next, we will calculate the Cost Function \(J \) when \(w =1 \). For this value of \(w \), it turns out that the error term inside the Cost Function is equal to 0 for each of the three data points. Therefore, for this particular dataset, when \(w =1 \), then the cost \(J =0 \).
On the right-hand side, we can now plot our Cost Function. Notice that because the Cost Function is a function of the parameter \(w \), the horizontal axis is labelled as \(w \), and the vertical axis is labelled as \(J \). So, here when \(w=1 \), the \(J=0 \).
Recall that the Cost Function is measuring the squared error or difference between the estimator value and the true value. Visually, you can see that in this example when \(w=1 \), the error or difference is equal to 0 for each of the 3 data points.
Let us take a look at another example where \(w=0.5 \). Here, we can clearly see the error. It is the gap between the actual value of \(y \) and the value that the function \(f \) predicted.
Now, we can again calculate the Cost Function \(J \) which is equal to 0.58. We’ll plot this Cost Function on the right-hand side.
Let’s take a look at another example when \(w=0 \). Here, the Cost Function \(J \) is equal to 2.3.
We can keep doing this for other values of \(w \). Since \(w \) can be any number, it can also be a negative value. For example, if \(w \) is negative 0.5, then the line \(f \) is a downward-sloping line. It turns out that when \(w \) is negative 0.5, then, you end up with an even higher cost, around 5.25.
You can continue computing the Cost Function for different values of \(w \) and plot them. It turns out that by computing a range of values, you can slowly trace out what the cost function \(J \) looks like.
As you can see this function has a global minimum value when the value of \(w \) is equal to 1 and the cost is equal to 0. This means that if we want to identify the weight value which minimizes the loss, we want to find a minimum of this function. To do this we will use a method called Gradient Descent. Let’s learn more about the application of Gradient Descent in the following section.
3. Applying Gradient Descent
To better understand the Gradient Descent algorithm, let’s imagine that you are standing at the top of the hill on a foggy day. Your goal is to reach the point located at the base of the hill. Since the fog is very thick, you can not see that point, but you know that you need to move towards the base of the hill. So, you will begin to move downhill taking big steps when the slope of the hill is bigger, and small steps when the slope becomes smaller until you reach that point.
Gradient Descent is one of the most commonly used Machine Learning Optimization methods. The goal of this algorithm is to minimize the Cost Function and to find optimal values for \(w \) and \(b \).
What we’re going to do is just to start off with some initial guesses for \(w \) and \(b \). In Linear Regression, it won’t matter too much what the initial values are, so a common choice is to set them both to 0. With the Gradient Descent algorithm, we will keep on changing the parameters \(w \) and \(b \) by a little, every time, to reduce the Cost Function \(J \) until hopefully \(J \) settles at or near a minimum. One thing to note is that for some functions, \(J \) may not be a bow shape or a hammock shape. It is possible to have more than one possible minimum.
Understanding The Mathematics
Now let’s dive more deeply into Gradient Descent to gain better intuition about what it’s doing and why it might make sense.
A Gradient Descent is a function that describes the slope of the tangent of the Cost Function. Here’s the formula for Gradient Descent.
$$ Gradient = \frac{dJ}{dw} $$
To update our parameters \(w \) and \(b \) we also need to calculate by how much we need to move. We can do this by using the following formula:
$$ w_{u} = w-\alpha \frac{dJ(w,b)}{dw} $$
$$ b_{u} = b-\alpha \frac{dJ(w,b)}{db} $$
This variable \(\alpha \) is called the learning rate. The learning rate controls how big of a step you take when updating the model’s parameters. The learning rate is usually a small positive number between 0 and 1. What \(\alpha \) does is that it basically controls how big of a step you take downhill. If \(\alpha \) is very large, then that corresponds to a very aggressive Gradient Descent procedure where you’re trying to take huge steps downhill. On the other hand, if \(\alpha \) is very small, then you’d be taking small baby steps downhill.
The term, \(\frac{dJ}{dw} \), is a derivative term.
Developing The Intuition
In order to better understand this, let’s use a slightly simpler example where we work on minimizing just one parameter. Let’s say that you have a cost function \(J \) of just one parameter \(w \). This means the Gradient Descent now looks like this.
$$ w_{u} = w-\alpha \frac{dJ(w)}{dw} $$
So, here we’re trying to minimize the cost by adjusting the parameter \(w \). Let’s look at what Gradient Descent does to the function \(J(w) \).
Here, on the horizontal axis, is our parameter \(w \), and on the vertical axis is the Cost. Now let’s initialize Gradient Descent with some starting value for \(w \). Gradient Descent will, now, update \(w \) using the following formula:
$$ w_{u} = w-\alpha \frac{dJ(w)}{dw} $$
Now, let’s look at what this derivative term means. A way to think about the derivative at this point on the line is to draw a tangent line, which is a straight line that touches this curve at that point. The slope of this line is the derivative of the function \(J \) at this point. To get the slope, you can draw a little triangle and compute the height divided by the width of the triangle. That is the slope. For example, this slope might be 2 over 1. When the tangent line is pointing up and to the right, the slope is positive, which means that this derivative is a positive number. The updated \(w_{u} \) is going to be equal to \(w \) minus the learning rate times some positive number.
$$ w_{u} = w-\alpha \cdot (positive) $$
Note that a learning rate is always a positive number. So, if you take \(w \) minus a positive number, you end up with a new value for \(w \), that’s smaller. On the graph, you’re moving to the left, you’re decreasing the value of \(w \). You may notice that this is the right thing to do if your goal is to decrease the cost \(J \), because when we move towards the left on this curve, the cost \(J \) decreases, and you’re getting closer to the minimum.
Now, let’s take the same function as above, but this time we will initialize gradient descent at a different location.
This line sloping down to the right has a negative slope. In other words, the derivative of \(J \) at this point is a negative number. This means you subtract from \(w \), a negative number. But subtracting a negative number means adding a positive number, and so you end up increasing \(w \). Because subtracting a negative number is the same as adding a positive number to \(w \). This step of Gradient Descent causes \(w \) to increase, which means you’re moving to the right of the graph. Again, it looks like Gradient Descent is doing something reasonable, and is getting you closer to the minimum.
Hopefully, these last two examples show some of the intuition behind what a derivative term is doing and why this host Gradient Descent changes \(w \) to get you closer to the minimum.
One other key quantity in the Gradient Descent algorithm is the learning rate \(\alpha \). How do you choose \(\alpha \)? What happens if it’s too small or what happens when it’s too big? Let’s take a deeper look at the parameter Alpha to help build intuition about what it does, as well as how to make a good choice for a good value of Alpha for your implementation of Gradient Descent.
Now that we have learnt about Cost Function and Gradient Descent, let’s apply this knowledge and try and implement a Linear Regression model in Python.
4. Implementing A Linear Regression Model In Python (From Scratch)
To begin with, we will define the LinearRegression class with two methods .fit( ) and .predict( ).
We create an instance of our LinearRegression class with training data as the input to the class and initialize the bias and constant values as 0.
The .fit( ) method in our class implements Gradient Descent wherein with each iteration we calculate the partial derivatives of the function with respect to parameters and then, update the parameters using the learning rate and the gradient value.
It turns out that if you calculate these derivatives, these are the terms you would get.
We will use these formulas to compute these two derivatives and implement Gradient Descent. Moreover, with the .predict( ) method we are simply evaluating the function \(y = w \cdot x + b \), using the optimal values of our parameters, in other words, this method estimates the line of best fit.
#Import required modules
import numpy as np
#Defining the class
class LinearRegression:
def __init__(self, x , y):
self.data = x
self.label = y
self.w = 0
self.b = 0
self.m = len(x)
def fit(self , epochs , lr):
#Implementing Gradient Descent
for i in range(epochs):
y_pred = self.w * self.data + self.b
#Calculating derivatives w.r.t Parameters
D_w = (-2/self.m)*sum(self.data * (self.label - y_pred))
D_b = (-1/self.m)*sum(self.label-y_pred)
#Updating Parameters
self.w = self.w - lr * D_w
self.b = self.b - lr * D_b
def predict(self , inp):
y_pred = self.w * inp + self.b
return y_pred
Now let’s again create the synthetic data points and plot them.
rng = np.random.RandomState(0)
X = 10 * rng.rand(50)
Y = 2 * X + 10 + rng.randn(50)
plt.figure(figsize = (10,6))
plt.scatter(x,y , color = 'green')
plt.xlabel('x' , size = 20)
plt.ylabel('y', size = 20)
plt.show()
Next, we are going to call the class LinearRegression() that we created. Then, we will use the .fit() method to train the model. We are going to train the model on 1,000 epochs and we are going to set the learning rate to be equal to 0.0001. Finally, we will use the predict function to calculate our estimated value.
#Creating the class object
regressor = LinearRegression(x,y)
#Training the model with .fit method
regressor.fit(1000 , 0.01) # epochs-1000 , learning_rate - 0.0001
#Prediciting the values
y_pred = regressor.predict(x)
#Plotting the results
plt.figure(figsize = (10,6))
plt.scatter(x,y , color = 'green')
plt.plot(x , y_pred , color = 'k' , lw = 3)
plt.xlabel('x' , size = 20)
plt.ylabel('y', size = 20)
plt.show(Visually, it seems that our straight line fits the data perfectly.
This brings us to the end of this tutorial about Linear Regression models, Cost Function and Gradient Descent. We also built a simple model in Python. We hope you could make an even better than us in no time.
Linear Regression Models In Machine Learning
- Linear Regression is one of the most popular and widely used Supervised Learning algorithms in the world today
- The two most important aspects of a Linear Regression model are Cost Function and Gradient Descent
- Average Squared Error Cost Function is used so that the Cost Function doesn’t get bigger as the training set gets bigger
- To minimize the Cost Function, Gradient Descent is used as a common Machine Learning Optimization method
- Gradient Descent is nothing but the slope of the tangent of the Cost Function
Summary
Another post, our second one, in our all-new Machine Learning tutorial series comes to an end. We hope you grasped the theory, the mathematics and the intuition behind the concepts you learned today. Why not try and build your own Linear Regression model at home? Let us know what problem you are trying to solve and your results. We’ll be excited to discuss it with you. In case you have any other doubts, feel free to reach out to us using the comments section below. We’ll see you soon with another exciting post. Till then, keep your learning rate high! 😉




